The Weirstrass Function
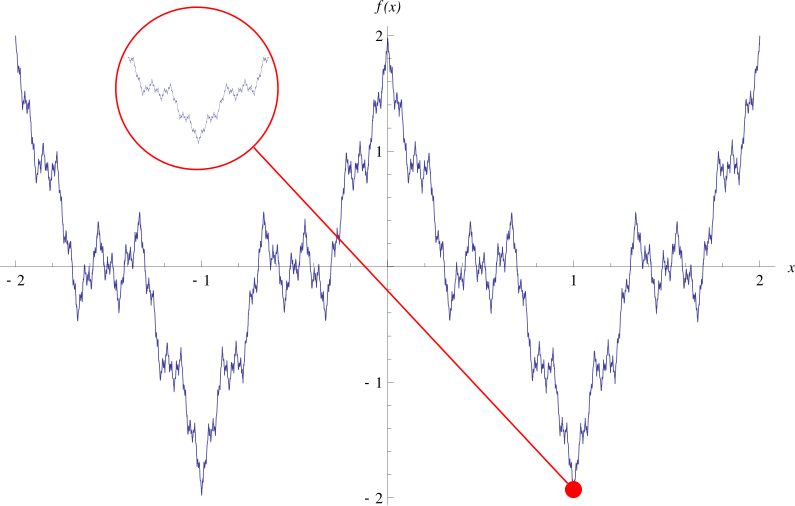 |
| The Weierstrass Function |
Nov. 9. I wondered about the following questions:
Do there exist monotonic functions that are everywhere continuous but nowhere differentiable?Do there exist monotonic functions that are nowhere continuous?
No in either case, it seems. Here is an answer:
First, monotone functions only can have a countable number of discontinuities (since these must be jump discontinuities where the function makes progress upward/downward and all uncountable positive sums are infinite).Moreover, for a more involved reason, the set of points where a monotone function is not differentiable must have lebesgue measure 0. (I.e. they are differentiable almost everywhere.)
One way to see this is from the fact that for an increasing function the limit of the slope of the secant line between (x,f(x)) and (x+h,f(x+h)) for each fixed x as h varies must always exist (and be nonnegative), provided we allow it to also take on the value +infinity. Then one can show this cannot be infinity except on a measure 0 set...again, the function would make too much progress.
On the other hand, the derivative can not exits on an uncountable set (e.g. the Cantor staircase function). Moreover, there is a slightly more sophisticated example of a strictly increasing continuous function that goes from f(0)=0 to f(1)=1 which has a derivative equal to 0 almost everywhere, in fact whenever the derivative exists.
Since they are differentiable almost everywhere, the derivatives of monotone functions are Lebesgue integrable functions (extend to the nondifferentiable points however you want, it won't affect the integral). So the previous example shows that the Fundamental Theorem of Calculus cannot be extended to even the class of derivatives of continuous monotone functions (even when the resulting derivative function is the constant function), since then we would have 0=\int_01 f'(x)dx=f(1)-f(0)=1. (The FTC does work, however, if f is continuous and the derivative exists except at a countable set).
From PlanetMathm here is Cantor's Staircase (in a 20-iteration figure, instead of infinite iterations), which uses a Cantor Set to build a function which is continuous and monotonic (strictly?) but with f'(x) =0 almost everywhere.
 |
| Graph of the cantor function using 20 iterations |
Labels: math
To view the post on a separate page, click:
at
11/08/2008 08:50:00 AM (the permalink).
![]()
![]()


<< Home